기록하는 곳

Dynamic Programming (동적 프로그래밍)

큰 문제를 작은 문제로 나누어 풀어 해를 저장해놓고 크기가 보다 큰 문제의 해를 점진적으로 풀어나가는 상향식 접근 방법.
분할되는 소문제들이 독립적일 필요가 없다.
최적성의 원리를 만족하는 문제에 대해서만 적용 가능하다.

Divide and Conquer(분할정복)과의 차이

재귀함수처럼 같은 값을 중복되게 연산할 필요가 없다.
(중복되는 문제에서 효율성이 더 좋음)

방법

모든 작은 문제들은 한번만 풀어야 한다.
작은 문제들은 풀 때마다 어딘가에 값을 저장해놓고 필요할 때 호출한다. (Memoization)

피보나치

재귀함수

def fibonacci(n):
  if n < 2:
    return n
  else:
    return fibonacci(n-1) + fibonacci(n-2)


print(fibonacci(10)) # 55

위의 코드는 재귀를 이용한 코드이다. fibonacci 함수가 같은 값들을 반복하며 연산하고 있다.

이런 불필요한 연산을 피하기 위해 한번 연산한 값을 저장해두는 것이다.

DP 이용

def fibonacci(n):
  if n <= 2:
    return 1

  if memo[n] != 0:
    return memo[n]

  memo[n] = fibo(n-1) + fibo(n-2)
  return memo[n]


print(fibonacci(10)) # 55

DP를 이용하면 푼 코드를 보면 memo라는 리스트에 값을 저장해놓는다.

DP는 Top-Down, Bottom-Up이라는 방식이 있는데 나중에 알아보도록 하자.

연쇄 행렬 곱셈 문제

여러 개의 행렬을 연속적으로 곱할 때 필요한 곱셈 연산의 최솟값을 구하는 문제가 주로 나온다.

행렬 6개(A1, A2, A3, A4, A5, A6)가 있다고 해보자.

예제

d = [5, 2, 3, 4, 7, 8, 9] d0 = A[1]의 행의 수 d1 = A[1]의 열의 수
...

A1 = d0 x d1 A2 = d1 x d2 ... A6 = d5 x d6

위의 문제에서 A4 x A5 x A6를 구하기 위한 방법은 두가지다.

A4 x A5 x A6

  1. (A4 x A5) x A6
  2. A4 x (A5 x A6)

1번을 풀어보자.

(A4 x A5)를 먼저 풀면 (A4 x A5) = (d3 x d4) x (d4 x d5) = d3 x d5가 된다.
위의 계산 과정에서 (d3 x d4) x (d4 x d5)의 곱셈 연산의 횟수는 d3 x d4 x d5로 표현된다.
그러면 계산해서 나온 d3 x d5에 A6 계산을 마저 해보자.

(d3 x d5) x (d5 x d6)로 표현할 수 있고 이 식의 곱셈 연산 횟수는 d3 x d5 x d6로 표현된다.

즉, 계산마다 알 수 있는 곱셈 연산의 횟수를 더하면 행렬 곰셈에 필요한 총 곱셈 횟수를 구할 수 있게 된다. (상향식 방법이란것도 여기서 증명됐다.)

최종적으로 전체 최솟값은 (d3 x d4 x d5) + (d3 x d5 x d6) = 512가 된다.


두 번째 경우의 수인 `A4 x (A5 x A6)도 풀어보자.

(A5 x A6)는 의 곱셈 연산 횟수는 d4 x d5 x d6 = 504가 된다. 행렬은 d4 x d6이 될 것이다.
A4까지 마저 계산하면, 식은 (d3 x d4) x (d4 x d6)이고 곱셈 연산 횟수는 d3 x d4 x d6 = 252가 된다. 두 연산 횟수를 더하면 504 + 252 = 756이 된다.


첫 번째 경우의 수랑 비교하면 512 < 756 이므로 첫번 째 경우의 수 (A4 x A5) x A6가 최소 곱셈 연산을 하는 것을 알 수 있다.

위의 풀이를 점화식으로 정리하면 다음과 같다.

점화식

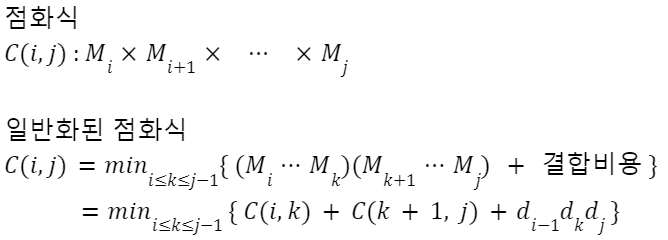
점화식-연쇄행렬곱셈

C(i, j)에서 i = j일 경우 C(i, j) = 0이라는 것도 알아두자.
오랜만에 행렬을 한다면 개념부터 헷갈릴 수도 있지만 막상 해보면 그렇게 어렵지는 않으니 점화식을 무작정 외우기 보다는 확실하게 이해하고 사용하자.

연쇄 행렬 곱셈 풀이의 시간 복잡도

O(n^3)


행렬 곱셈의 최소 연산 횟수를 구하는 문제 말고도, 최소 곱셈 연산 횟수를 도출하기 위한 k를 주어진 행렬들을 이용하여 전부 구하는 문제도 있다.

연쇄 행렬 곱셈의 최소 곱셈 연산 횟수를 얻기 위해 사용되는 k는 P라는 테이블(=행렬?)에 저장하여 문제를 푼다.

즉, P(i, j) = k가 된다.

스트링 편집 거리 (두 문자열의 편집 거리)

문자열 X를 Y로 변환하는 데 필요한 전체 편집 연산에 대한 최소 비용이다.

문자열을 string이 아닌 char[]로 보는 것이 좀 더 이해가 쉬울 것이다.

문자열 X, Y의 부분 문자열 사이의 편집거리는 아래와 같다.

  1. X의 마지막 글자가 삭제된 경우
  2. Y의 마지막 글자가 삽입된 경우
  3. X의 마지막 글자가 Y의 마지막 글자와 같거나 같도록 변경된 경우

점화식은 아래와 같다.
첫 번째 문자부터 마지막 이전까지의 문자의 편집거리에서 마지막 문자를 삽입하거나 제거하는데 이에 대한 비용이 델타P, 델타I이다.
점화식의 세 번째 식은 마지막 문자가 변경될 경우이다. 마지막 문자가 같은 경우에는 비용이 0, 다른 경우에는 변경이 필요하므로 비용이 델타C가 든다.

점화식

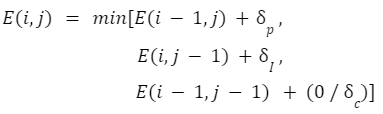
점화식-스트링편집거리

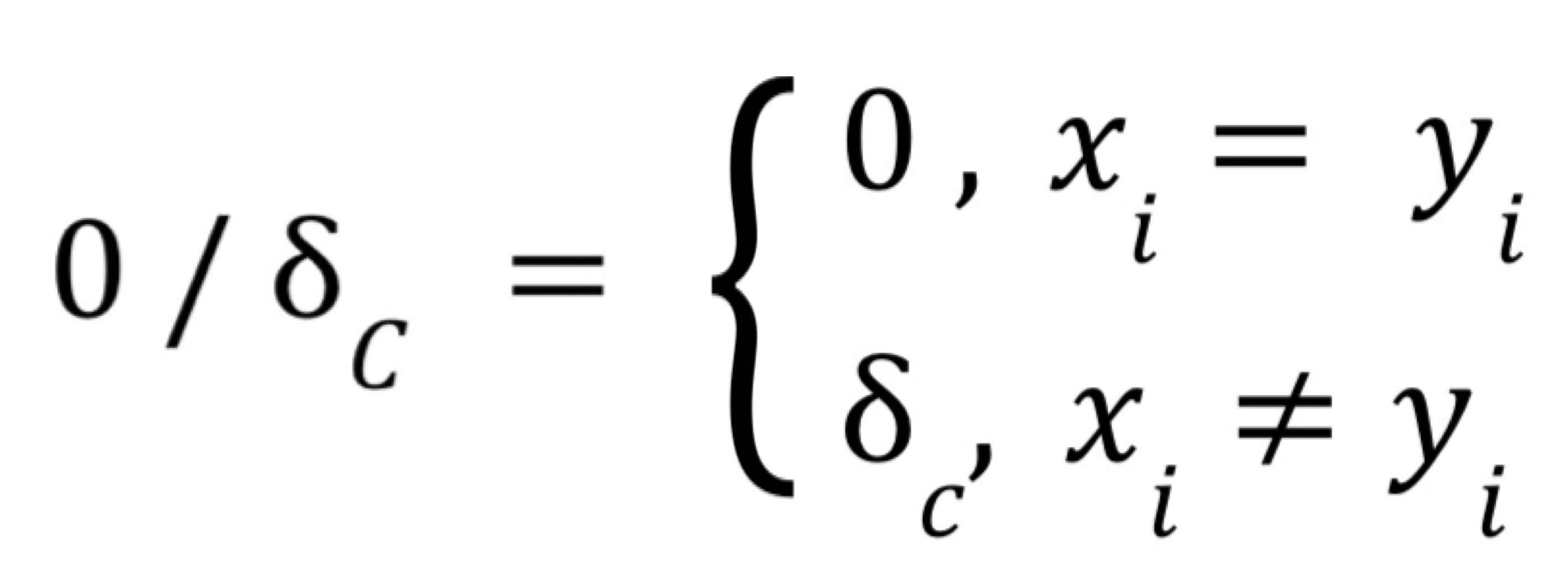
풀이

X = bbabb, Y = abaa 의 스트링 편집 거리를 구해보자. 표로 정리하면 다음과 같다.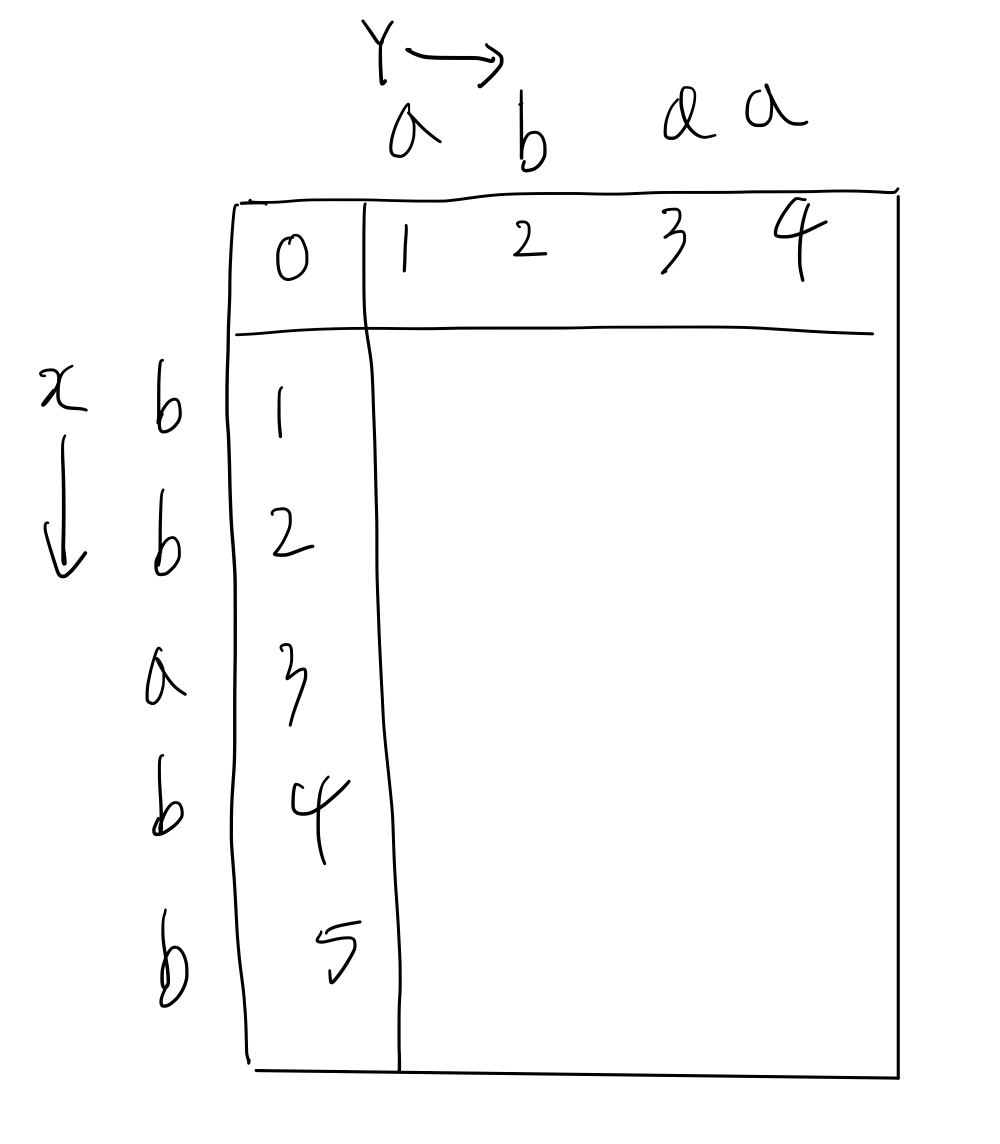

X의 첫 번째 문자 b, Y의 첫 번째 문자 a의 편집 거리 부터 구해보자.
b와 a는 다른 문자이므로 변경이 일어날 경우에는 비용이 2가 된다.
그 외에 삽입, 삭제는 비용이 1이다. 즉, 아래와 같다.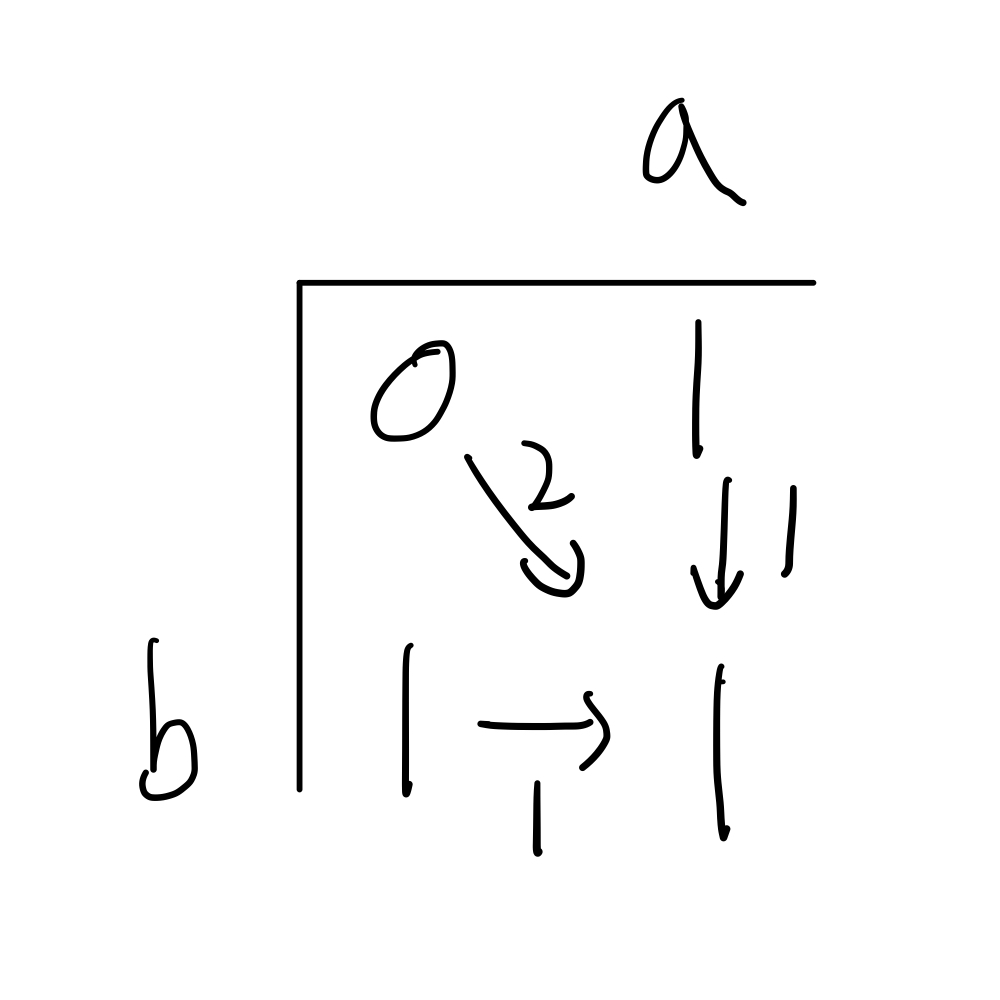

이런 식으로 계속해서 테이블을 채워 나가면 아래와 같아진다.
즉, X와 Y의 스트링 편집 거리는 5가 된다.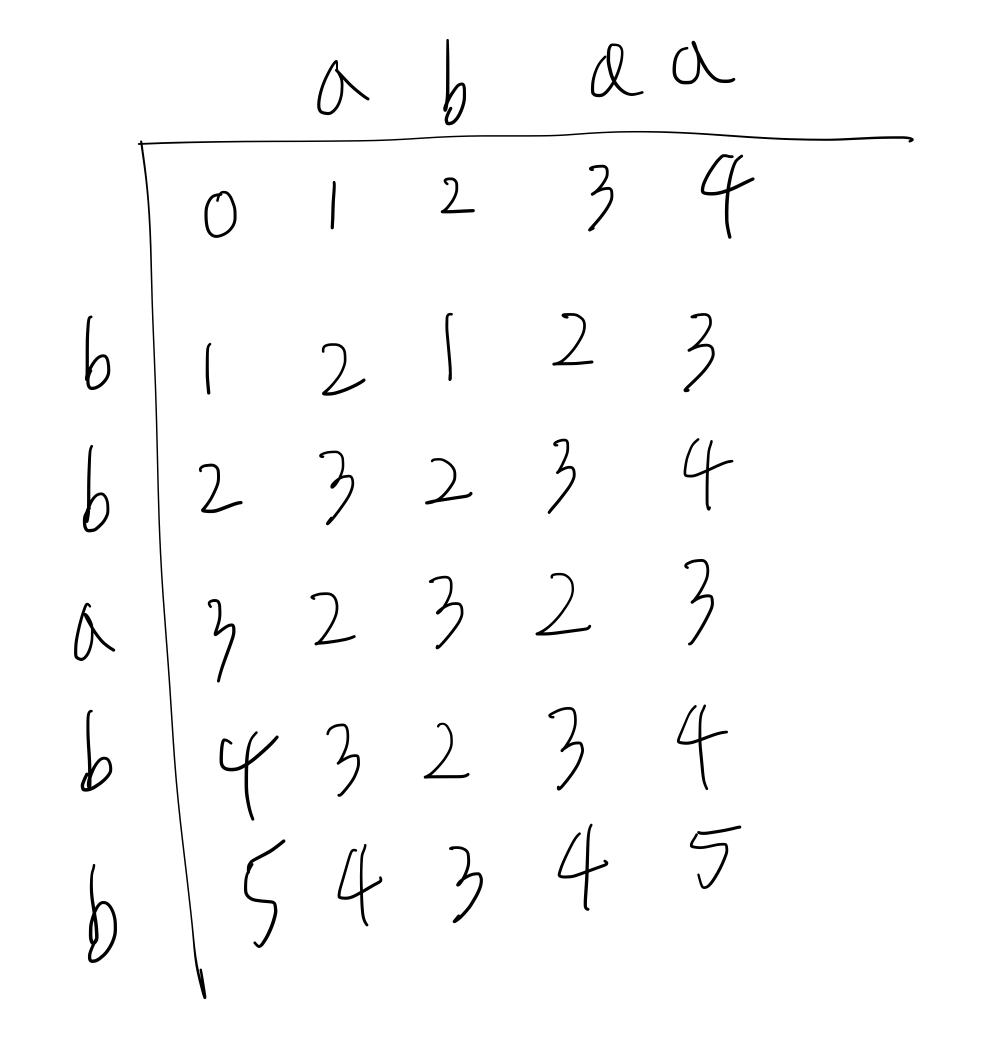

어떤 연산을 통해 최솟값이 나왔는지 저장하는 P(i,j)

위의 문제를 예로 들자면, 스트링 편집 거리의 최솟값이 5가 나오기 위해 어떤 연산을 거쳤는지 기록하는 행렬을 P(i,j)라고 한다.

Last Updated: