기록하는 곳

행렬 테두리 회전하기

목차

문제

문제를 풀다가 이 글을 찾아오신 분들이 대다수라 생각되어 접어놓았습니다.

문제를 보실 분들은 클릭해주세요!!

문제 설명

rows x columns 크기인 행렬이 있습니다. 행렬에는 1부터 rows x columns까지의 숫자가 한 줄씩 순서대로 적혀있습니다. 이 행렬에서 직사각형 모양의 범위를 여러 번 선택해, 테두리 부분에 있는 숫자들을 시계방향으로 회전시키려 합니다. 각 회전은 (x1, y1, x2, y2)인 정수 4개로 표현하며, 그 의미는 다음과 같습니다.

x1 행 y1 열부터 x2 행 y2 열까지의 영역에 해당하는 직사각형에서 테두리에 있는 숫자들을 한 칸씩 시계방향으로 회전합니다.
다음은 6 x 6 크기 행렬의 예시입니다.

grid_example

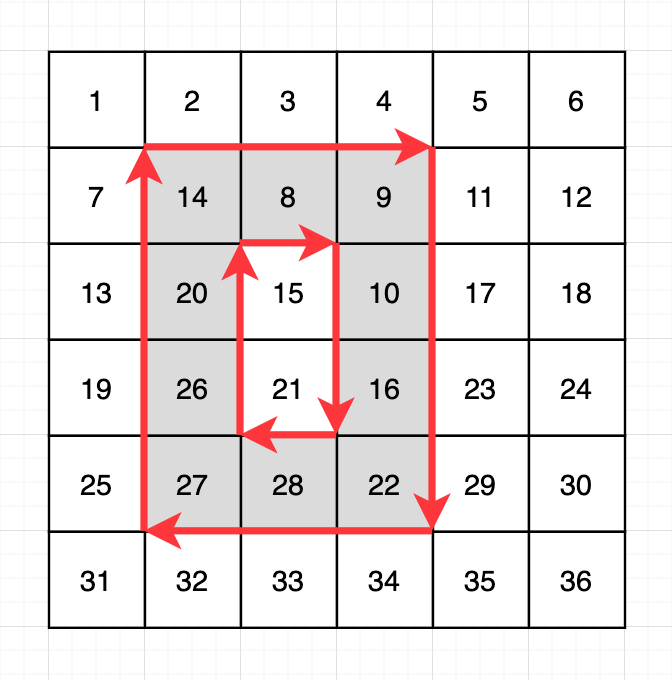
이 행렬에 (2, 2, 5, 4) 회전을 적용하면, 아래 그림과 같이 2행 2열부터 5행 4열까지 영역의 테두리가 시계방향으로 회전합니다.
이때, 중앙의 15와 21이 있는 영역은 회전하지 않는 것을 주의하세요.

rotation_example

행렬의 세로 길이(행 개수) rows, 가로 길이(열 개수) columns, 그리고 회전들의 목록 queries가 주어질 때,
각 회전들을 배열에 적용한 뒤, 그 회전에 의해 위치가 바뀐 숫자들 중 가장 작은 숫자들을 순서대로 배열에 담아 return 하도록 solution 함수를 완성해주세요.

제한 사항

- rows는 2 이상 100 이하인 자연수입니다. - columns는 2 이상 100 이하인 자연수입니다. - 처음에 행렬에는 가로 방향으로 숫자가 1부터 하나씩 증가하면서 적혀있습니다. - 즉, 아무 회전도 하지 않았을 때, i 행 j 열에 있는 숫자는 ((i-1) x columns + j)입니다. - queries의 행의 개수(회전의 개수)는 1 이상 10,000 이하입니다. - queries의 각 행은 4개의 정수 [x1, y1, x2, y2]입니다. - x1 행 y1 열부터 x2 행 y2 열까지 영역의 테두리를 시계방향으로 회전한다는 뜻입니다. - 1 ≤ x1 < x2 ≤ rows, 1 ≤ y1 < y2 ≤ columns입니다. - 모든 회전은 순서대로 이루어집니다. - 예를 들어, 두 번째 회전에 대한 답은 첫 번째 회전을 실행한 다음, 그 상태에서 두 번째 회전을 실행했을 때 이동한 숫자 중 최솟값을 구하면 됩니다.

입출력 예시

| rows | columns | queries | result | |:---:|:---:|:---:|:---:| | `6` | `6` | `[[2,2,5,4],[3,3,6,6],[5,1,6,3]]` | `[8, 10, 25]` | | `3` | `3` | `[[1,1,2,2],[1,2,2,3],[2,1,3,2],[2,2,3,3]]` | `[1, 1, 5, 3]` | | `100` | `97` | `[[1,1,100,97]]` | `[1]` |

입출력 예 설명

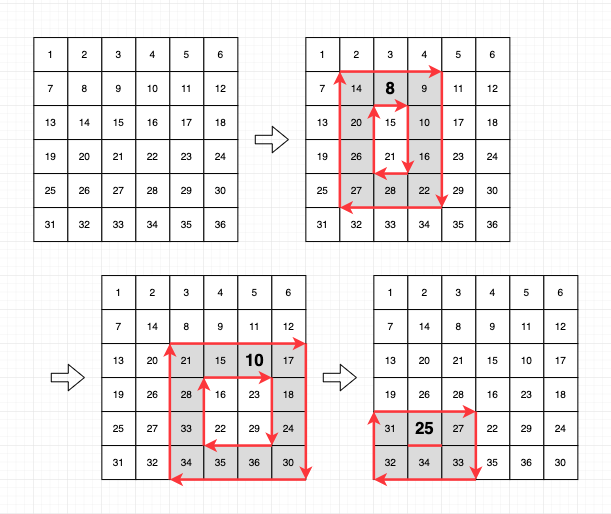
입출력 예 #1

  • 회전을 수행하는 과정을 그림으로 표현하면 다음과 같습니다.
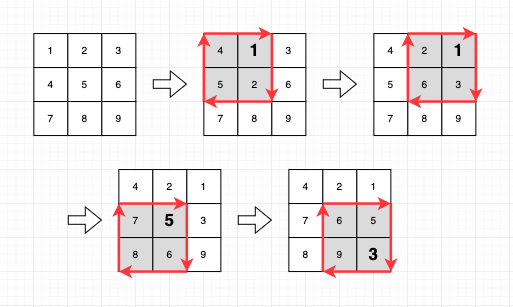
    rotation_example

입출력 예 #2

  • 회전을 수행하는 과정을 그림으로 표현하면 다음과 같습니다.
    rotation_example

입출력 예 #3

  • 이 예시에서는 행렬의 테두리에 위치한 모든 칸들이 움직입니다. 따라서, 행렬의 테두리에 있는 수 중 가장 작은 숫자인 1이 바로 답이 됩니다.

풀이 방법

회전을 수행할 행렬부터 만들어줬다.
행렬을 만드는 로직은 solution 함수 내에서 작성했고 회전하는 로직은 따로 분리하였다.

행렬 테두리를 회전하는 함수 rotation 은 회전한 후 가장 작은 수를 return 한다.

회전하는 테두리의 좌표값인 [x1, y1, x2, y2]를 [2, 2, 5, 4]라고 하자.

1. 테두리의 왼쪽 부분부터 위로 한칸씩 이동

단, 이동시키기 전에 가장 윗부분인 8을 변수에 보관해놓는다.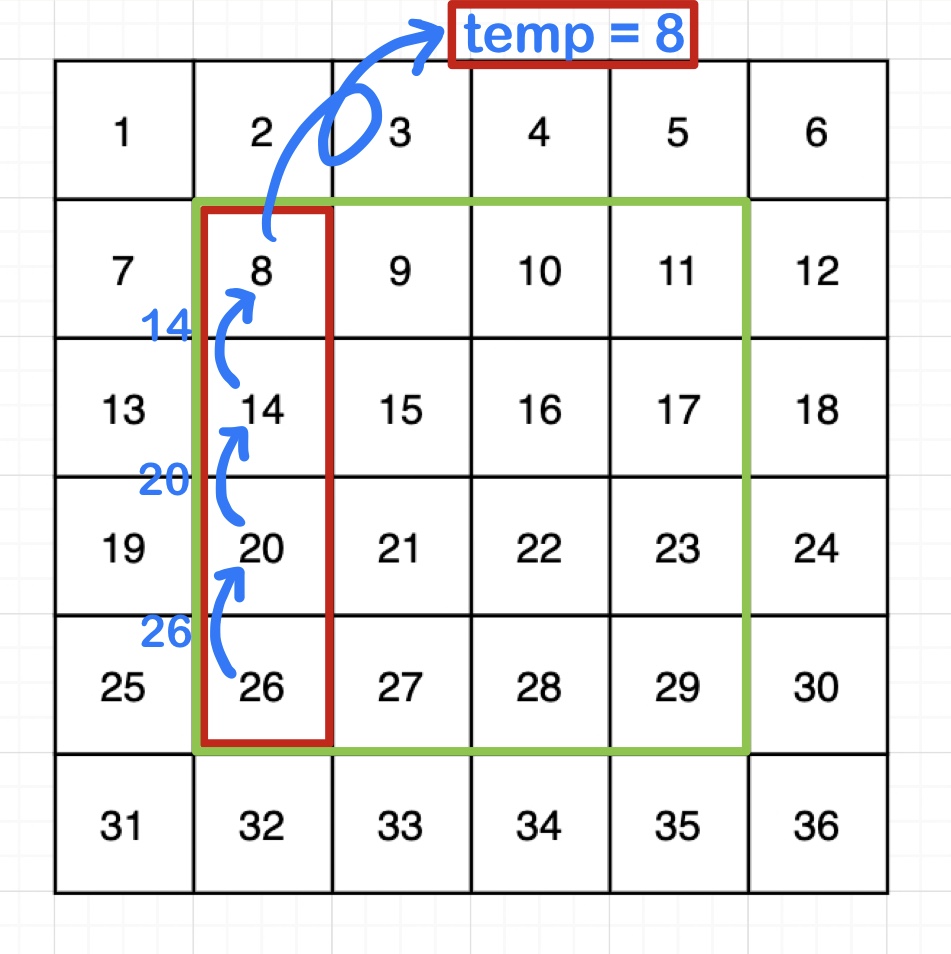

해당 로직을 코드로 표현하면 다음과 같다.
위에서 설명한 것과 다르게 minNum이 추가되어 있는데 회전할 때 마다 최솟값을 체크하기 위함이다.

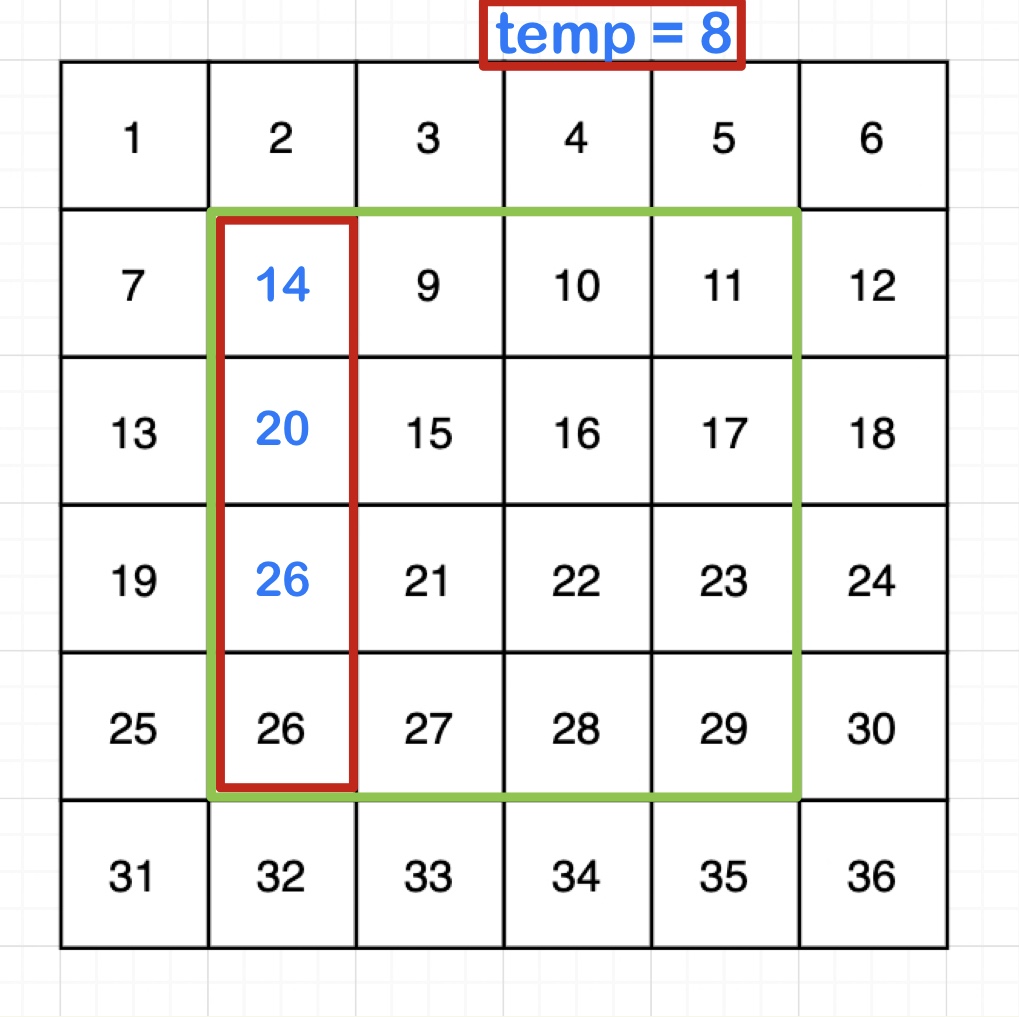
const temp = grid[x1][y1]; // 8
let minNum = temp; // 가장 작은 수는 일단 8로 초기화

for (let i = x1; i < x2; i++) {
  grid[i][y1] = grid[i + 1][y1]; // ex) 8의 자리에 14를 넣어줌
  minNum = min(grid[i + 1][y1], minNum); // min(a,b) = a와 b 중 작은 수 return
}

이동하고 나면 아래와 같이 변경된다.

2. 이어서 아랫쪽 -> 오른쪽 -> 위쪽 순서로 시계방향 회전

로직은 위에서 설명했으니 그림으로 대체하겠다.
temp와 minNum 변수 선언 부분은 위에서 이미 했으니 for문만 분기마다 반복시켜주면 된다.

1. 아랫쪽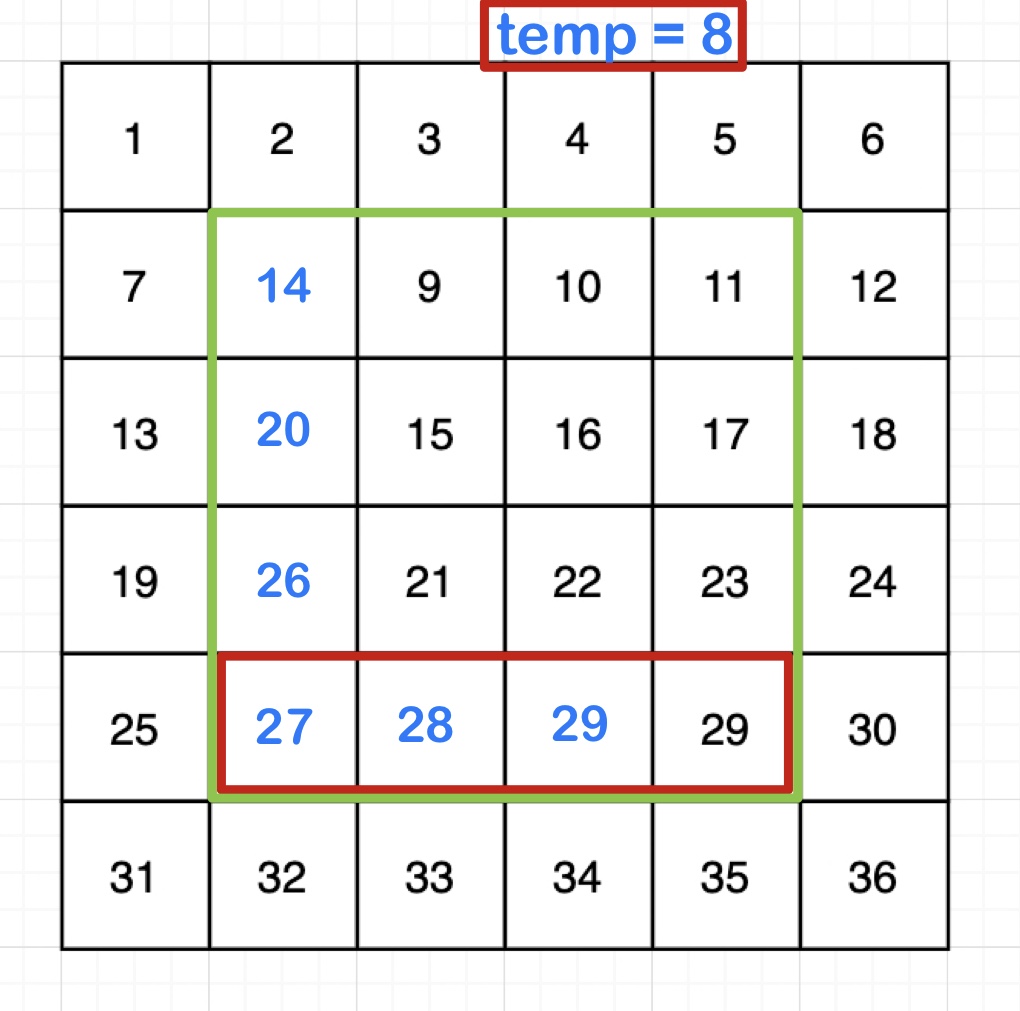

2. 오른쪽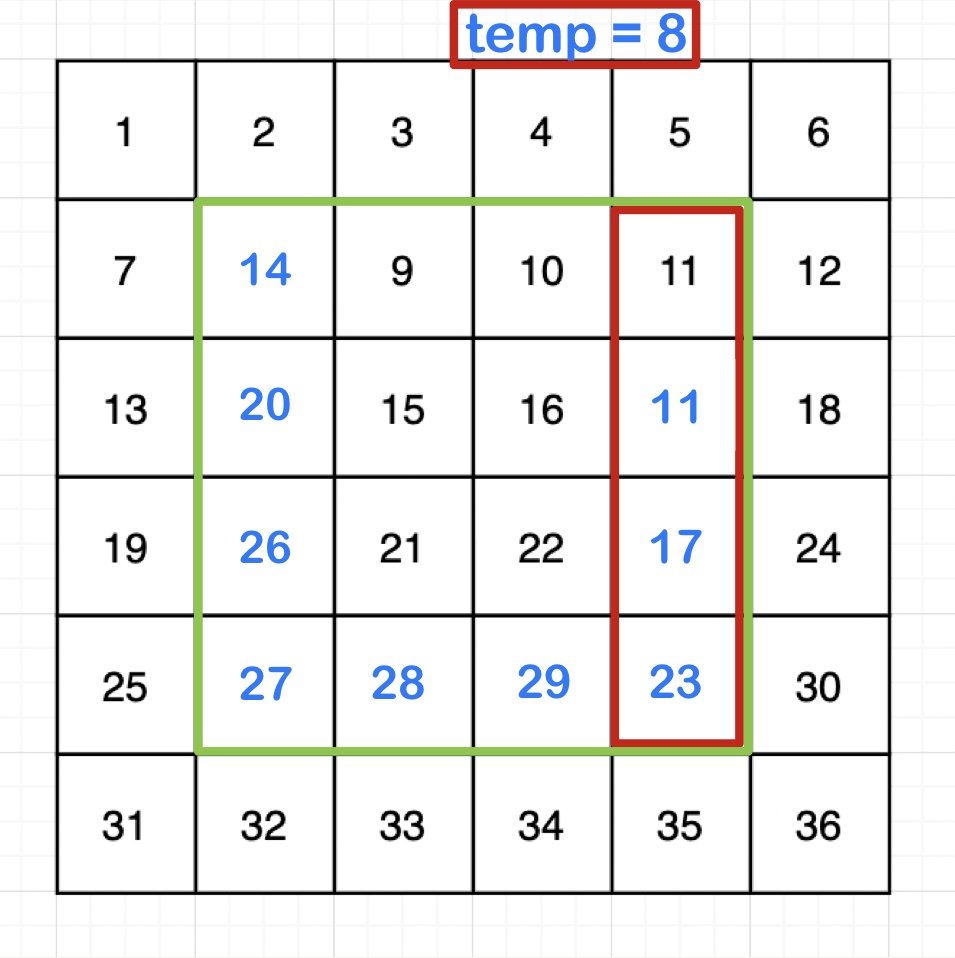

3. 윗쪽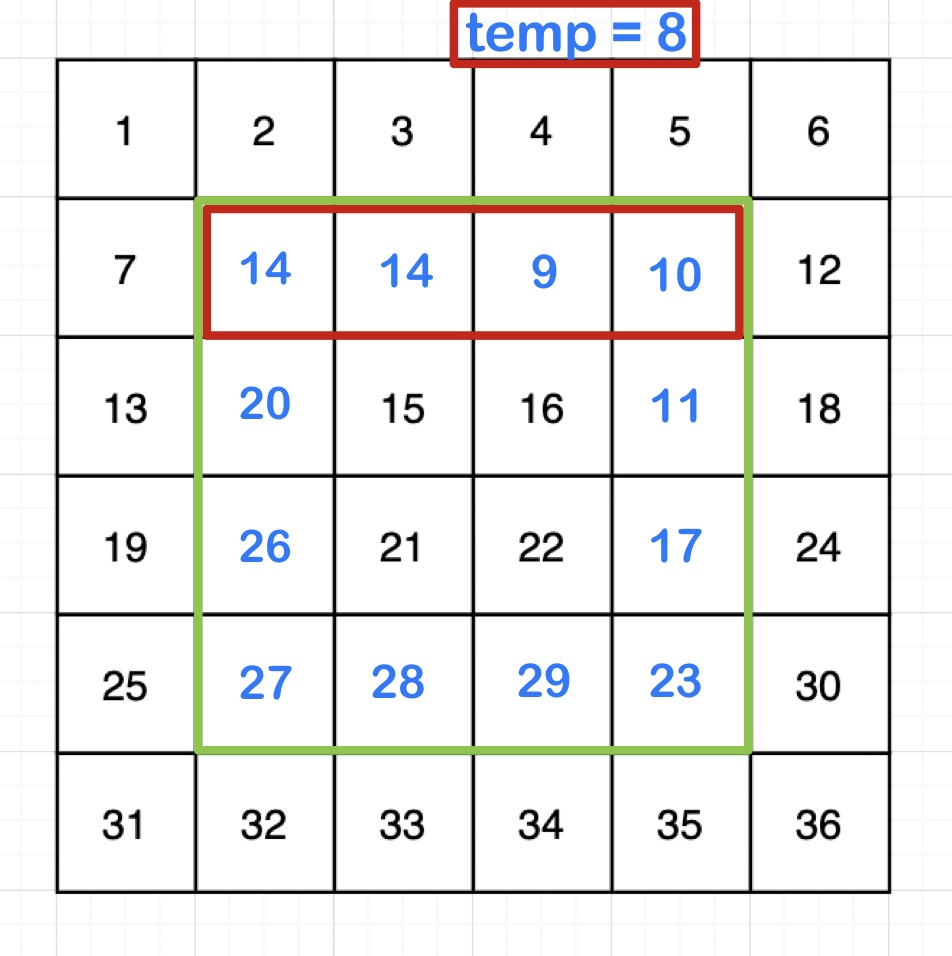

회전은 다 끝냈다.
이제 temp에 넣어놓았던 8을 [x1][y1+1] 위치에 넣어주자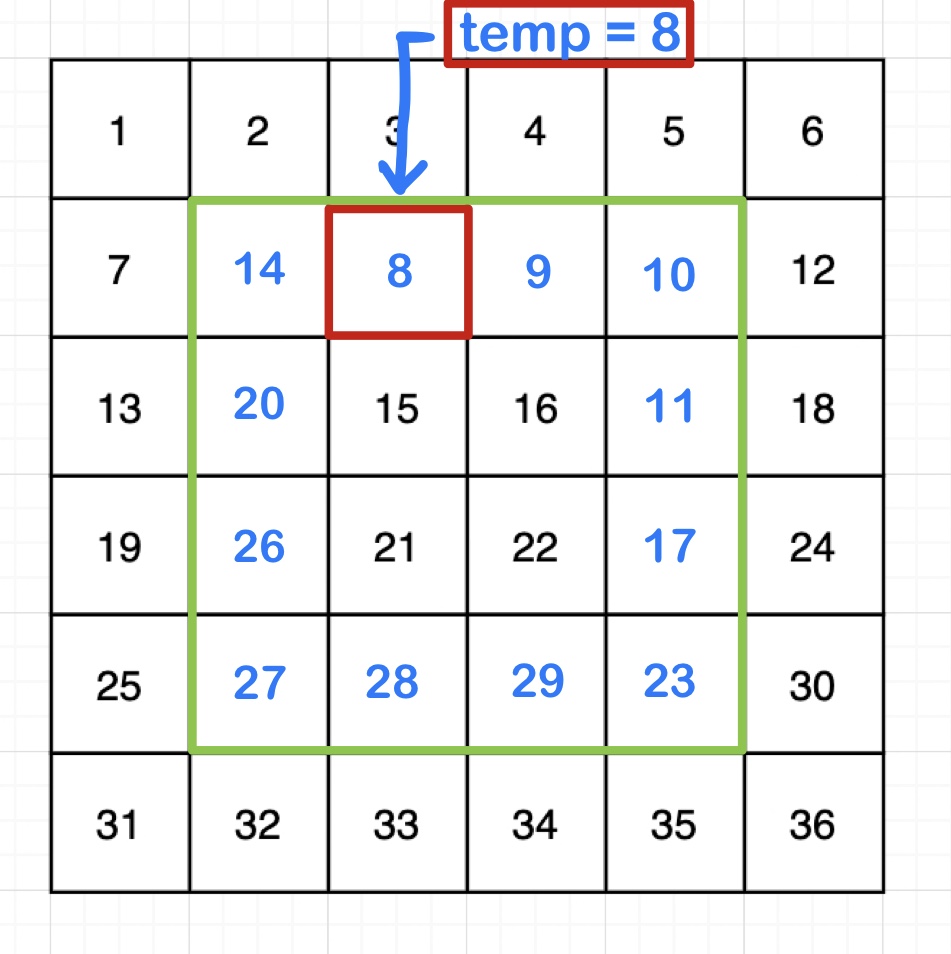

for문을 돌면서 계산된 minNum을 answer 배열에 넣어주자.

answer.push(minNum);

전체 코드

solution 함수

function solution(rows, columns, queries) {
  const grid = []; // rows * columns 행렬
  let cnt = 1; // 행렬을 순회하며 1 ~ rows*columns 만큼 넣어줌

  // 행렬 만드는 로직
  for (let x = 0; x < rows; x++) {
    const row = [];
    for (let y = 0; y < columns; y++) {
      row.push(cnt++);
    }
    grid.push(row);
  }

  return queries.map((query) => rotation(grid, query));
}

min 함수 (어떤 수가 작은지 비교해서 리턴해줌)

const min = (a, b) => (a > b ? b : a); // 어떤 수가 작은지 비교함

rotation 함수 (행렬 회전 후 가장 작은 수 return)

const rotation = (grid, [x1, y1, x2, y2]) => {
  x1--;
  y1--;
  x2--;
  y2--; // 인덱스에 맞게 -1씩 해줌
  const temp = grid[x1][y1]; // 좌측 상단의 수를 저장해놓자.
  let minNum = temp; // 가장 작은 수는 일단 좌측상단으로 초기화

  for (let i = x1; i < x2; i++) {
    // 좌측 (아랫쪽의 숫자를 위로 이동)
    grid[i][y1] = grid[i + 1][y1];
    minNum = min(grid[i + 1][y1], minNum);
  }

  for (let i = y1; i < y2; i++) {
    // 하단 (오른쪽의 숫자를 왼쪽으로 이동)
    grid[x2][i] = grid[x2][i + 1];
    minNum = min(grid[x2][i + 1], minNum);
  }

  for (let i = x2; i > x1; i--) {
    // 우측 (윗쪽의 숫자를 아래로 이동)
    grid[i][y2] = grid[i - 1][y2];
    minNum = min(grid[i - 1][y2], minNum);
  }

  for (let i = y2; i > y1; i--) {
    // 상단 (왼쪽의 숫자를 오른쪽으로 이동)
    grid[x1][i] = grid[x1][i - 1];
    minNum = min(grid[x1][i - 1], minNum);
  }

  grid[x1][y1 + 1] = temp; // (x1, y1+1) 좌표에 temp(x1, y1)을 넣어줌으로써 마무리

  return minNum; // 가장 작은 수를 push!
};

제출 코드

열기
function solution(rows, columns, queries) {
  // 행렬 만드는 로직
  const grid = [];
  let cnt = 1;

  for (let x = 0; x < rows; x++) {
    const row = [];
    for (let y = 0; y < columns; y++) {
      row.push(cnt++);
    }
    grid.push(row);
  }

  return queries.map((query) => rotation(grid, query));
}

// 어떤 수가 작은지 비교함
const min = (a, b) => (a > b ? b : a);

// 로테이션 함수는 회전 후 가장 작은 수를 리턴해줌
const rotation = (grid, [x1, y1, x2, y2]) => {
  x1--;
  y1--;
  x2--;
  y2--; // 인덱스에 맞게 -1씩 해줌
  const temp = grid[x1][y1]; // 좌측 상단의 수를 저장해놓자.
  let minNum = temp; // 가장 작은 수는 일단 좌측상단으로 초기화

  for (let i = x1; i < x2; i++) {
    // 좌측 (아랫쪽의 숫자를 위로 땡김)
    grid[i][y1] = grid[i + 1][y1];
    minNum = min(grid[i + 1][y1], minNum);
  }

  for (let i = y1; i < y2; i++) {
    // 하단 (오른쪽의 숫자를 왼쪽으로 땡김)
    grid[x2][i] = grid[x2][i + 1];
    minNum = min(grid[x2][i + 1], minNum);
  }

  for (let i = x2; i > x1; i--) {
    // 우측 (윗쪽의 숫자를 아래로 땡김)
    grid[i][y2] = grid[i - 1][y2];
    minNum = min(grid[i - 1][y2], minNum);
  }

  for (let i = y2; i > y1; i--) {
    // 상단 (왼쪽의 숫자를 오른쪽으로 땡김)
    grid[x1][i] = grid[x1][i - 1];
    minNum = min(grid[x1][i - 1], minNum);
  }

  grid[x1][y1 + 1] = temp; // (x1, y1+1) 좌표에 temp(x1, y1)을 넣어줌으로써 마무리

  return minNum; // 가장 작은 수를 push!
};
Last Updated: